

ここでは卒業研究について説明していきます。僕のテーマは量子限界まで安定化されたレーザー光源の開発です。タイトルに量子限界とかかっこいい感じの名前がありますが、 実際卒業研究中に体調を崩してしまいうまく研究を進めることはできませんでした。(なので研究したところまで書きます。結果が出てないですが許してください)
ここでは研究の動機について説明していきます。僕の研究では主にレーザー光に焦点を当てて研究をしました。レーザー光は、力・角速度・時間などの精密測定には欠かすことができないものです。 そのためレーザー光は重力波検出器や量子測定などの精密測定によく応用されています。これらの精密測定への応用において、レーザー光自体が持つ古典的な揺らぎが測定の邪魔をし、大きな課題となっています。 特に測定周波数帯域が低いような場合(典型的にはMHzよりも低い場合)では、その影響は顕著に表れるようになります。先ほど紹介した重力波検出器や量子計測は、測定周波数が低周波数帯域であるのでレーザー光源の安定化を 行うことはとても重要になっています。ここではレーザー光の雑音を雑音のページで導出した相対強度雑音で定量的に評価していきます。
それでは実験の内容を説明していきます。まず大まかな実験の流れ空です。本研究の目的はレーザー光源の安定化でした。そこで、能動的なフィードバック制御でレーザー光源の強度を安定化するシステムを構築し、
その性能評価をすることを目指しました。しかし、最初に述べましたが、今回の卒業研究では僕の体調不良が原因で真のレーザー強度雑音の安定度を評価することができませんでした。(ここでいう“真の”とはアウトオブループから実験データを評価できなかったことを指す。後に詳しく説明する)
僕が行ったのは、制御系の構築、フィルターをデジタル回路で自作、それを用いて能動的なフィードバック制御によるレーザー強度安定化、そして一巡伝達関数の測定によって制御でレーザー強度雑音をどのくらい安定化できるかを見積もる(インループの測定結果を用いて)までです。それではこれらについて詳しく説明していきます。
まず強度安定化をどのように行ったのかについてです。
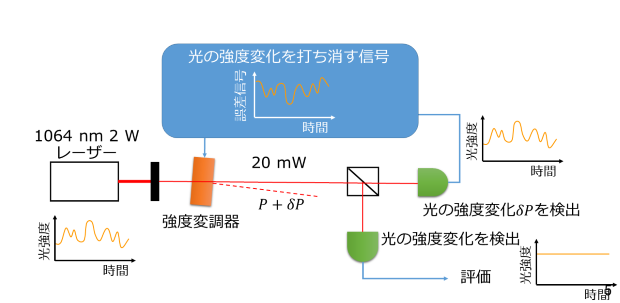
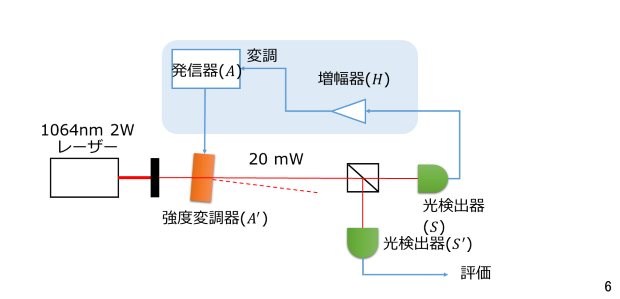
ここではマイケルソン干渉計にファブリペロー共振器を組み込んだファブリペローマイケルソン干渉計の重力波に対する応答について説明します。
まず始めに、ファブリペロー共振器の説明をしていきます。ファブリペロー共振器とは2枚の鏡を向かい合わせることによって光を往復させることができる装置のことです。
左側よりレーザーが入射されます。共振器の左側の鏡をフロントミラー、右側の鏡をエンドミラーと呼びます。この2枚の鏡の距離をLとします。フロントミラーの反射率、透過率をそれぞれ$t_{F}$、$r_{F}$とし、
エンドミラーの反射率、透過率をそれぞれ$r_{E}$、$t_{E}$とします。またフロントミラーに入射する電場を$E_i$、反射する電場を$E_r$、エンドミラーを透過する電場を$E_t$としています。
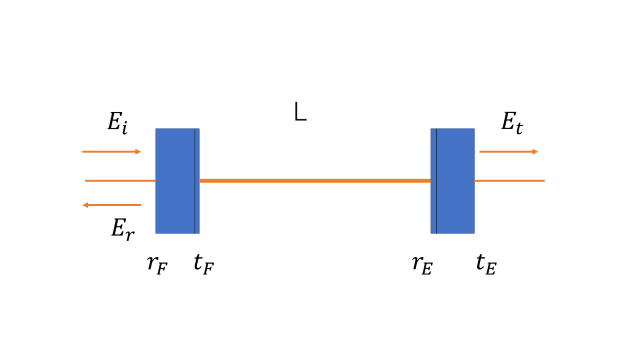
まず反射光の振幅を考えてみます。共振器内での往復を考えると以下のように求まります。 \begin{align*} E_r &= E_i(-r_F)+E_i t^2_F r_E e^{-i\phi}+E_i t^2_F r^2_E r_F i^{-2i\phi} + E_i t^2_F r^2_E r^2_F e^{-3i\phi}+…… \\ &= E_i(-r_F) + E_i t^2_F r_E i^{-i\phi}\sum_{n=0}^{\infty}\left(r_F r_E e^{-i\phi}\right)^n \\ &= E_i\left(-r_F+\frac{t^2_F r_E e^{-i\phi}}{1-r_F r_E e^{-i\phi}}\right) \end{align*} ここで$\phi$は光が共振器を往復するときの位相変化を表していて、レーザーの角周波数を$\omega$とすると$\phi = \frac{2L\omega}{c}$となります。 同様にして透過光の振幅も考えます。 \begin{align} E_t &= E_i t_F t_E e^{-\frac{i\phi}{2}}+E_i t_F r_E r_F t_E e^{-\frac{3i\phi}{2}}+E_i t_F r^2_E r^2_F t_E e^{-\frac{5i\phi}{2}}+…… \\ &= E_i t_F t_E e^{-\frac{i\phi}{2}}\sum_{n=0}^{\infty}\left(r_F r_E e^{-i\phi}\right)^n \\ &= E_i\frac{t_F t_E e^{-\frac{i\phi}{2}}}{1-r_E r_F e^{-i\phi}} \end{align} 以上二つの式より、ファブリペロー共振器の反射率$r_{cav}$と透過率$t_{cav}$は \begin{align} r_{cav}(\phi) &= -r_F+\frac{t^2_F r_E e^{-i\phi}}{1-r_F r_E e^{-i\phi}} \\ t_{cav}(\phi) &= \frac{t_F t_E e^{-\frac{i\phi}{2}}}{1-r_F r_E e^{-i\phi}} \end{align} となります。また、透過光と反射光の振幅より透過光と反射光の強度$P_i$と$P_r$を求めることができます。以下ではそれを示します。 \begin{align} P_t &= |E_r|^2 &= \frac{|(t_F^2+r_F^2)r_E-r_F)|^2+4r_F r_E (t_F^2+r_F^2)\sin^2(\phi/2)}{(1-r_F r_E)^2+4r_E r_F \sin^2(\phi/2)}|E_i|^2 \end{align} \begin{align} P_i &= |E_i|^2 &= frac{(t_F t_E)^2}{(1-r_E r_F)^2+4r_E r_F \sin^2(\phi/2)}|E_i|^2 \end{align} 透過光強度$P_i$が最大になるとき共振器内の光強度が最大になるときで、入射光とファブリペロー共振器が共振しているということができます。 この共振条件は$\phi = 2\pi m $(mは自然数)となります。これは$P_i$の式の分母が最小になることから明かです。この条件を光の周波数と波長の関係を用いれば$2L = m\lambda$(mは自然数) と書き直すことができます。この式から共振条件は共振器の往復長がレーザー波長$\lambda$の整数倍になっていることがわかります。 これらのことを踏まえてフリースペクラルレンジ(FSR)とフィネスを導出していきます。 まずFSRについてです。これは共振と共振の間の周波数差$\nu_{FSR}=\frac{c}{2\pi}$のことを言います。 次にフィネスについて説明していきます。これは共振器内の光がどれくら往復できるかを示したものになります。フィネスを求めるためにはFSRと透過強度ピークの半値全幅$\nu_{FWHM}$の比をとる必要があります。 そこで$\nu_{FWHM}$を求めます。これは透過光強度$P_i$を用いて求めることができます。 \begin{equation} \frac{1}{1+\frac{4r_F r_E}{(1-r_F r_E)^2}\sin^2\left(\frac{\pi L \nu_{FWHM}}{c}\right)}=\frac{1}{2} \end{equation} この式を$\frac{\pi L \nu_{FWHM}}{c}=\frac{\pi \nu_{FWHM}}{2\nu_{FSR}} << 1$として解くと$\sin$の展開ができるので \begin{equation} \nu_{FWHM}=\frac{c(1-r_F r_E)}{2\pi L \sqrt{r_E r_F}} \end{equation} となります。よってフィネス$\mathcal{F}=\frac{\nu_{FSR}}{\nu_{FWHM}}=\frac{\pi\sqrt{r_E r_F}}{1-r_E r_F}$と求まりました。 ここで共振器の分類について少しふれておきます。共振器に用いる鏡の反射率の大小関係によって三種類の分類がされます。