ここでは伝達関数について説明していきます。
前回入出力関係を2つの方法で数学的に示しました。そこで、まず入出力関係を運動方程式で表したn回微分方程式のラプラス変換を
考えてみます。
\begin{equation}
(s^n + a_{n-1}s^{n-1} +...+a_1s + a_0)Y(s)=(b_ms^m + b_{m-1}s^{m-1} + ...+b_1s+b_0)X(s)
\end{equation}
これはラプラス変換後のn回微分方程式です。この式から入出力の比を取ります。
\begin{equation}
G(s) = \frac{Y(s)}{X(s)} = \frac{b_ms^m + b_{m-1}s^{m-1} + ...+b_1s+b_0}{s^n + a_{n-1}s^{n-1} +...+a_1s + a_0}
\end{equation}
このように定義される関数を伝達関数と呼びます。簡単に言うと入出力の比を周波数空間で考えた関数です。
それでは、伝達関数の性質についてみていきましょう。まず、伝達関数の分母と分子に注目します。分母が0となるときの解を極といい、分子が0となるときの解を零点といいます。
これが何を意味するかは今後話を進めていく中でわかってきます。次に、分母と分子の次数に注目します。分子より分母の次数が大きければプロパー、分子より分母の次数が小さければインプロパーといいます。
今回はプロパーな場合の伝達関数を取り扱います。
それでは、次に畳み込み積分のラプラス変換を考えます。
\begin{equation}
Y(s)=G(s)X(s)
\end{equation}
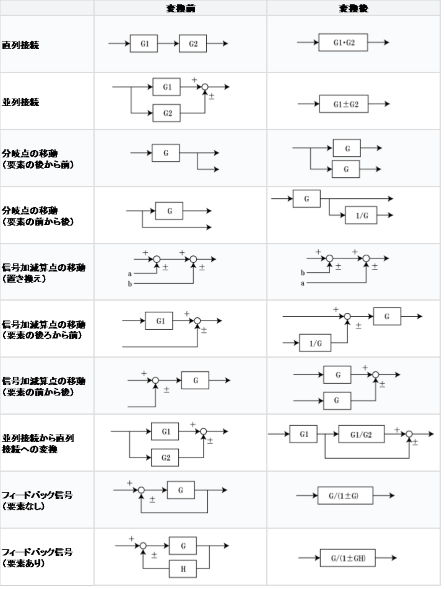
すると、入出力関係を伝達関数の積で書くことができるようになります。この関係をブロックを使って表したものをブロック線図といいます。
以下に様々なブロック線図の書き方をまとめた表を示しておきます。