

本ページでは雑音について説明していきます。干渉計の感度を向上させるためには様々な雑音を特定し、低減しなければいけません。雑音の原因は様々ありますが、 大きく分けて4つの原因があります。以下にそれを示します。
ここではまず雑音の定式化を行っていきます。そもそも雑音は不規則に現れる物理量です。このような物理量を定量的に評価する方法として二乗平均平方(RMS)という計算手法があります。 これは、ある物理量$x(t)$を測定した際に、値の2乗の時間平均をとり、平方根をとるという計算です。以下にそれを示します。 \begin{equation} RMS := \sqrt{\frac{1}{T}\int_{-T/2}^{T/2}dt x^2(t)} \end{equation} これは今時間空間で定義されています。重力波検出器の雑音は周波数空間で議論するのが一般的なので、周波数空間に拡張する必要があります。 ここでパワースペクトル密度というものを考えます。これは簡単に言えばRMSを時間空間から周波数空間に拡張したものです。以下でこのことについて詳しく説明していきます。 まず周波数空間で議論するためにフーリエ変換と逆フーリエ変換を以下のように定義します。 \begin{align} x(t) &= \frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega\hat{X}(\omega)e^{i\omega t}\\ \hat{X}(\omega) &= \int_{-\infty}^{\infty}dt x(t)e^{-i\omega t} \end{align} それではここから詳しく議論していきます。最初に測定値$x(t)$が実数であると仮定します。すると$x(t)=x*(t)$が成り立つことがわかります。よって \begin{align} x(t)-x^*(t) &= \frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega\hat{X}(\omega)e^{i\omega t}-\frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega\hat{X}^*(\omega)e^{-i\omega t}\\ &= \frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega(\hat{X}(\omega)-\hat{X}^*(-\omega))e^{i\omega t} = 0 \end{align} となります。この関係式から$\hat{X}(\omega) = \hat{X}^*(-\omega)$が成り立ちます。ここで時系列データの範囲がいま$-\infty < t < \infty$で定義されているところを、実用性を考慮して $-\frac{T}{2} < t < \frac{T}{2}$の有限の範囲で定義し直します。するとフーリエ変換を以下のように定義し直すことができます。 \begin{equation} \hat{X}(\omega) = \int_{-T/2}^{T/2}dt x(t) e^{-i\omega t} \end{equation} これを用いて時間空間でのRMSを周波数空間に拡張していきます。まず以下にRMSの両辺を2乗したものを示します。 \begin{equation} RMS^2 = \frac{1}{T}\int_{-T/2}^{T/2}dt x^2(t) \end{equation} 定義し直したフーリエ変換より \begin{align} \frac{1}{T}\int_{-T/2}^{T/2}dt x^2(t) &= \frac{1}{T}\int_{-T/2}^{T/2}dt x(t) \frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega \hat{X}(\omega)e^{i\omega t}\\ &= \frac{1}{T}\int_{-\infty}^{\infty}d\omega\hat{X}(\omega)(\frac{1}{2\pi}\int_{-T/2}^{T/2}dt x(t)e^{i\omega t})^*\\ &= \frac{1}{T}\int_{-\infty}^{\infty}d\omega\hat{X}(\omega)(\hat{X}(\omega))^*\\ &= \frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega\frac{|\hat{X}(\omega)|^2}{T}\\ &= \frac{1}{2\pi}\int_{-\infty}^{\infty}d\omega P(\omega)\\ P(\omega) &= \frac{|\hat{X}(\omega)|^2}{T} \end{align} となります。こうして求まったPをパワースペクトル密度といいます。 パワースペクトル密度は測定した実効値のうちある周波数成分がどれくらい寄与しているかを表しています。ちなみにパワースペクトル密度の平方根を振幅スペクトル密度といいます。 こうしてパワースペクトル密度を求めることができ、雑音の定式化ができました。 それでは次からはいくつかの雑音について述べていきたいと思います。
ここでは地面振動の雑音について説明します。地面振動は地上にある重力波検出器の低周波数帯の感度を制限します。典型的な地面振動の振幅スペクトル密度の値が知られており
\begin{equation}
\delta x(f) \sim 10^{-7}\times\left(\frac{1[Hz]}{f}\right)^2 [m/\sqrt{Hz}]
\end{equation}
となります。重力波検出器では鏡を振り子でつるすことによってこの地面振動の雑音の影響を小さくしています。それでは振り子でつるすことによってどの程度地面振動雑音を抑えられるのかを
見積もってみたいと思います。今回は簡単のために1段の振り子を考えます。また、鏡を質点近似し質量をm[kg]とし、振り子の全長をL[m]、重力加速度をg[m/s^2]、振り子のダンピング係数を$\Gamma_m$[N/(m/s)]とします。
そして振り子の固定点が微小距離x[m]だけ変位したときの質点の変位y[m]を求めます。
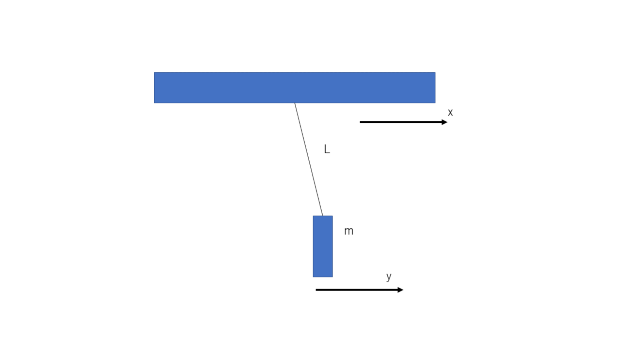
それではこの問題を解いていきます。まずこの系の運動方程式を以下に示します。 \begin{equation} m\ddot{y} = \frac{mg}{L}(x-y)-\Gamma_m(\dot{x}-\dot{y}) \end{equation} ここで$\gamma_m = \Gamma_m/2m$、$\omega_m^2=g/L$と定義して運動方程式を書き換えると \begin{equation} m\ddot{y}=m\omega_m^2(x-y)-2m\gamma_m(\dot{x}-\dot{y}) \end{equation} となります。この運動方程式はいま時間空間なのでフーリエ変換をします。 \begin{align} -\omega^2m Y &= m\omega_m^2 (X-Y) -2m\gamma_m (-i\omega X -i\omega Y)\\ -\omega^2m Y + m\omega_m^2 Y -2i m \omega \gamma_m Y &= (m\omega_m^2 + 2im\omega \gamma_m)x\\ Y &= \frac{m\omega_m^2 + 2im\gamma_m\omega}{m(-\omega^2 + \omega_m^2)+2im\gamma_m\omega}\\ Y &= \frac{\omega_m^2 + i\frac{\omega_m\omega}{Q_m}}{-\omega^2 + \omega_m^2+ i\frac{\omega_m\omega}{Q_m}}\\ \end{align} ここでx、yのフーリエ変換をしたものをX、Yとし、$Q_m = \omega_m/2\gamma_m$とします。ここで測定している周波数帯が振り子の共振周波数$\omega_m$に比べ十分に大きく($\omega >> \omega_m$)、振り子のQ値が十分に大きいとき($Q_m >> \omega\omega_m$) \begin{equation} Y \approx \frac{\omega_m^2}{\omega^2}x \end{equation} と近似できます。このときの地面振動の影響は \begin{equation} |\delta y(f)| \approx \frac{f_m^2}{f^2} |\delta x(f)| \end{equation} となり、振り子の効果によって周波数の2乗分の軽減効果がついていることがわかります。 今回は1段のときを考えましたが、重力波検出器ではこの振り子を何段も用いた防振をして防振性能を高めています。
ここでは輻射圧雑音について説明します。光子は運動量を持つので光子数が変化すると鏡が受ける反作用が変わり鏡を揺らします。これを光子の引き起こす輻射圧雑音といいます。 重力波検出器における輻射圧雑音の振幅スペクトル密度は以下のようになります。 \begin{equation} x_{RP}(f) = \frac{2\mathcal{F}}{\pi m f^2}\sqrt{\frac{2\hbar I}{\pi^3 c \lambda}} \end{equation} ここでmは鏡の質量、Iは干渉計に入射したレーザーの強度、$\lambda$はレーザーの波長、$\mathcal{F}$は干渉計の腕のフィネスを表しています。この式から輻射圧雑音は 周波数の2乗で減衰し、鏡の質量が大きいほど小さくなることがわかります。
ここでは熱雑音について説明します。熱雑音は搖動散逸定理によって引き起こされます。熱雑音のパワースペクトル密度は\\ \begin{equation} S_{f,th}(\omega) = 4k_b T \gamma_m m(\hbar \omega << k_b T) \end{equation} となります。ここでは簡単のために減衰力が速度に比例すると仮定し議論していきます。これをviscos modelといいます。(減衰力が速度に比例しない場合は少し複雑になります) まず振り子の運動方程式を考えます。(振り子の運動の模式図より) \begin{equation} m\ddot{x} = -m\omega_m^2 x + \Gamma_m \dot{x} + F_{th} \end{equation} F_{th}は熱浴から受ける揺動力です。$\Gamma_m = 2m\gamma_m$、$\gamma_m = \omega_m/{2Q}$とおきました。この運動方程式をさらにフーリエ変換して整理すると \begin{equation} X(\omega) = \frac{1}{m(\omega_m^2 - \omega^2 +2i\gamma_m\omega)}\tilde{F}_{th}(\omega) \end{equation} となります。ここで$\chi_m(\omega) := 1/m(\omega_m^2 - \omega^2 + 2i\gamma_m\omega)$を力に対する感受率として定義します。パワースペクトル密度をこの感受率を用いて 振幅スペクトル密度に変換することを考えます。感受率の単位は[m/N]でパワースペクトル密度の単位は[N^2/Hz]です。一方で振幅スペクトル密度の単位は[m^2/Hz]です。つまり 以下のようにパワースペクトル密度に感受率の絶対値の2乗を乗じてやれば振幅スペクトル密度を求めることができます。 \begin{equation} S_{x,th} = |\chi_m(\omega)|^2 S_{f,th} = \frac{1}{m}\frac{4k_b T \gamma_m}{m(\omega_m^2 -\omega^2 + 2i\gamma_m \omega)} \end{equation} 特に測定周波数帯域が共振周波数と比べ十分に小さい場合は \begin{equation} \delta x_{th} = \sqrt{2S_{x,th}} \approx \sqrt{\frac{4k_b T}{m\omega_m^3 Q}} (\omega << \omega_m) \end{equation} となります。逆に測定周波数帯域が共振周波数と比べて十分に大きい場合は \begin{equation} \delta x_{th} = \sqrt{2S_{x,th}} \approx \sqrt{\frac{4k_b T \omega_m}{m\omega_m^4 Q}} (\omega >> \omega_m) \end{equation} となります。 また、減衰力が速度によらず一定な場合の熱雑音を以下に示します。これをstructure modelといいます。まず測定周波数帯域が共振周波数と比べ十分に小さい場合は \begin{equation} \delta x_{th} \approx \sqrt{\frac{4k_b T \phi_k(\omega)}{m\omega_m^2 \omega}}(\omega << \omega_m) \end{equation} となります。逆に測定周波数帯域が共振周波数と比べて十分に大きい場合は \begin{equation} \delta x_{th} \approx \sqrt{\frac{4k_b T \omega_m^2 \phi_k(\omega)}{m\omega^5 }}(\omega >> \omega_m) \end{equation} となります。ここで出てきた$\phi_k$は複素ばね定数というものです。ここでは深入りしないことにします。経験的に振り子の熱雑音はstructure modelに従うことが知られています。 また実際の重力波検出器では振り子の共振周波数が数Hz、鏡の機材の弾性振動が数十kHz、観測帯域が数百Hzであるので振り子の熱雑音は \begin{equation} \delta x_{th} \approx \sqrt{\frac{4k_b T \omega_m^2 \phi_k(\omega)}{m\omega^5 }} \end{equation} となり、鏡の熱雑音はモデル(viscus modelとstructure model)に応じて使い分ける必要があります。