

前章で説明した通り重力波は計量の1次の摂動項として現れ、波動方程式に従って伝搬するということを説明しました。 ここでは重力波をどのように検出するかを説明します。簡単のために重力波の+モードについてのみ考えていることに注意してください。 $\times$モードにつては座標を45度回転させることで+モードと同様の結果を得られます。
計量テンソル$\eta_{\mu\nu}$を用いると、光の4次元線素$ds^2=0$を表すことができます。 \begin{equation} ds^2=\eta_{\mu\nu}dx^{\mu}dx^{\nu}=0 \end{equation} となります。重力波によってこの計量テンソルは1次の摂動を受けます。そのため空間距離が微小ですが変化します。 これを4次元線素を用いて書くと \begin{equation} ds^2=(\eta_{\mu\nu}+h_{\mu\nu})dx^{\mu}dx^{\nu}=-(cdt)^2+(1+h_{\times}\exp i(-\omega t +kz))dx^2+(1-h_{\times}\exp i(-\omega t +kz))dy^2 +dz^2 \end{equation} となります。ここでどのような時空を考えても光の4次元線素の値は0になります。 \begin{equation} 0=-(cdt)^2+(1+h_{\times}\exp i(-\omega t +kz))dx^2+(1-h_{\times}\exp i(-\omega t +kz))dy^2 +dz^2 \end{equation} よってx軸方向を進む光は微小時間$dt$の間に \begin{equation} dx=\frac{c}{\sqrt{1+h_{\times}\exp i(-\omega t +kz)}}dt \end{equation} だけ進みます。簡単のために重力波の位相が$2\pi$であったとすると、 \begin{equation} dx=\frac{c}{\sqrt{1+h_{\times}}}dt \end{equation} となり、重力波が存在しないときに比べ時空が縮んでいることがわかります。一方でy軸方向に関しては \begin{equation} dy=\frac{c}{\sqrt{1-h_{+}}}dt \end{equation} となり、重力波が存在しない時よりも時空が伸びていることがわかります。 つまり重力波は、互いが90度をなす空間の長さを差動に変化させます。
重力波をとらえるには重力波の引き起こす差動変化を読み取ればいいことがわかります。そこで重力波検出器ではマイケルソン干渉計を用いてこの差動変化を
測定します。マイケルソン干渉計を以下に示します。
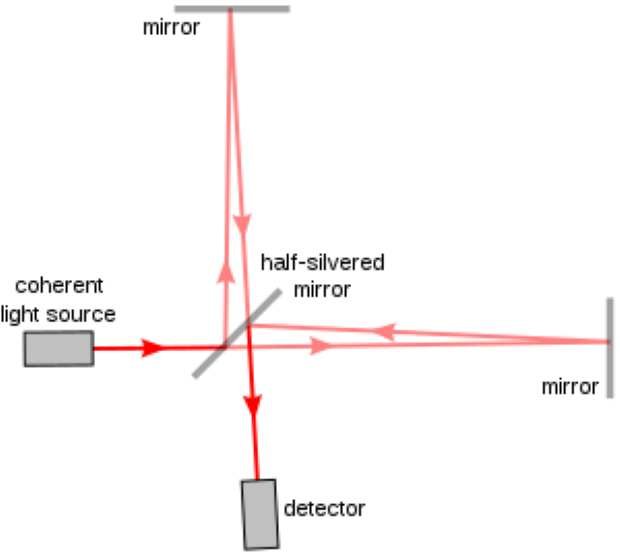
マイケルソン干渉計とはレーザー光源から出た光をビームスプリッタで互いに直交する方向に分け、それぞれの方向の先に 鏡をおき、光を打ち返してビームスプリッタ上で再度結合させる実験装置になっています。再度結合が起こるときに光は干渉します。 重力波は互いが90度をなす空間の長さを差動に変化させるので、マイケルソン干渉計の干渉条件を変化させます。よってマイケルソン干渉計の干渉状態を 常に測定していれば、重力波が干渉計に入射したときの差動変化を捉えることができるのです。それでは原理について詳しく説明していきたいと思います。 左側より入射されたレーザーはビームスプリッタでx軸方向とy軸方向に分けれられます。ビームスプリッタの裏面と表面との間で位相が$\pi$だけ異なります。 またx軸、y軸方向の基線長をそれぞれL_{x},L_{y}とします。そしてビームスプリッタを座標の原点とします。重力波が存在しなければx軸方向の光路を往復してきた光と、 y軸方向の光路を往復してきた光の位相差は \begin{equation} \phi_{x}-\phi_{y}=\frac{2(L_x-L_y)}{c}\Omega_0 \end{equation} ここでcは光速、$\Omega$はレーザーの角周波数です。重力波が存在すると空間の長さが変化するので光の位相差は次のように変化します。 \begin{equation} \phi_{x}-\phi_{y}=\frac{2(L_x-L_y)}{c}\Omega_0+\phi_{GM} \end{equation} ここで$\phi_{GM}$は重力波による位相差です。具体的な形は以下のようになります。 \begin{equation} \phi_{GM}=\int_{-\infty}^{\infty}d\omega H_{MI}(\omega)h(\omega)e^{i\omega t} H_{MI}(\omega)=\frac{2\Omega}{\omega}\sin\left(\frac{L\omega}{c}\right)e^{-i\frac{L\omega}{c}} \end{equation} $H_{MI}$はマイケルソン干渉計の重力波に対する周波数応答関数です。ここで$L_{x}=L_{y}=L$としています。 この式は角周波数$\omega$の重力波がマイケルソン干渉計に入射した際、その振幅が$H_{MI}$だげ増幅(or減衰)されて測定されることを意味しています。 $H_{MI}$から角周波数$\omega$の重力波をマイケルソン干渉計を用いて検出したいとき、その最適な基線長Lは \begin{equation} \frac{L\omega}{c}=\frac{\pi}{2} \Rightarrow L=\frac{\pi c}{2\omega} \end{equation} となります。仮に重力波の周波数が100Hzだったとすると基線長Lはおおよそ750kmとなり、地上でこれだけの干渉計を建設するのは 困難です。そこで考えられたのが干渉計の内部に光共振器を組み込み、実効的に基線長を伸ばすというアイディアです。 そこで次にマイケルソン干渉計に光共振器を組み込んだファブリペローマイケルソン干渉計について説明します。
ここではマイケルソン干渉計にファブリペロー共振器を組み込んだファブリペローマイケルソン干渉計の重力波に対する応答について説明します。
まず始めに、ファブリペロー共振器の説明をしていきます。ファブリペロー共振器とは2枚の鏡を向かい合わせることによって光を往復させることができる装置のことです。
左側よりレーザーが入射されます。共振器の左側の鏡をフロントミラー、右側の鏡をエンドミラーと呼びます。この2枚の鏡の距離をLとします。フロントミラーの反射率、透過率をそれぞれ$t_{F}$、$r_{F}$とし、
エンドミラーの反射率、透過率をそれぞれ$r_{E}$、$t_{E}$とします。またフロントミラーに入射する電場を$E_i$、反射する電場を$E_r$、エンドミラーを透過する電場を$E_t$としています。
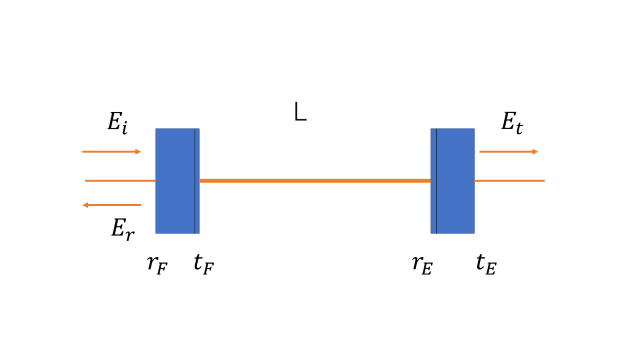
まず反射光の振幅を考えてみます。共振器内での往復を考えると以下のように求まります。 \begin{align} E_r &= E_i(-r_F)+E_i t^2_F r_E e^{-i\phi}+E_i t^2_F r^2_E r_F i^{-2i\phi} + E_i t^2_F r^2_E r^2_F e^{-3i\phi}+…… \\ &= E_i(-r_F) + E_i t^2_F r_E i^{-i\phi}\sum_{n=0}^{\infty}\left(r_F r_E e^{-i\phi}\right)^n \\ &= E_i\left(-r_F+\frac{t^2_F r_E e^{-i\phi}}{1-r_F r_E e^{-i\phi}}\right) \end{align} ここで$\phi$は光が共振器を往復するときの位相変化を表していて、レーザーの角周波数を$\omega$とすると$\phi = \frac{2L\omega}{c}$となります。 同様にして透過光の振幅も考えます。 \begin{align} E_t &= E_i t_F t_E e^{-\frac{i\phi}{2}}+E_i t_F r_E r_F t_E e^{-\frac{3i\phi}{2}}+E_i t_F r^2_E r^2_F t_E e^{-\frac{5i\phi}{2}}+…… \\ &= E_i t_F t_E e^{-\frac{i\phi}{2}}\sum_{n=0}^{\infty}\left(r_F r_E e^{-i\phi}\right)^n \\ &= E_i\frac{t_F t_E e^{-\frac{i\phi}{2}}}{1-r_E r_F e^{-i\phi}} \end{align} 以上二つの式より、ファブリペロー共振器の反射率$r_{cav}$と透過率$t_{cav}$は \begin{align} r_{cav}(\phi) &= -r_F+\frac{t^2_F r_E e^{-i\phi}}{1-r_F r_E e^{-i\phi}} \\ t_{cav}(\phi) &= \frac{t_F t_E e^{-\frac{i\phi}{2}}}{1-r_F r_E e^{-i\phi}} \end{align} となります。また、透過光と反射光の振幅より透過光と反射光の強度$P_i$と$P_r$を求めることができます。以下ではそれを示します。 \begin{align} P_t &= |E_r|^2 &= \frac{|(t_F^2+r_F^2)r_E-r_F)|^2+4r_F r_E (t_F^2+r_F^2)\sin^2(\phi/2)}{(1-r_F r_E)^2+4r_E r_F \sin^2(\phi/2)}|E_i|^2 \end{align} \begin{align} P_i &= |E_i|^2 &= frac{(t_F t_E)^2}{(1-r_E r_F)^2+4r_E r_F \sin^2(\phi/2)}|E_i|^2 \end{align} 透過光強度$P_i$が最大になるとき共振器内の光強度が最大になるときで、入射光とファブリペロー共振器が共振しているということができます。 この共振条件は$\phi = 2\pi m $(mは自然数)となります。これは$P_i$の式の分母が最小になることから明かです。この条件を光の周波数と波長の関係を用いれば$2L = m\lambda$(mは自然数) と書き直すことができます。この式から共振条件は共振器の往復長がレーザー波長$\lambda$の整数倍になっていることがわかります。 これらのことを踏まえてフリースペクラルレンジ(FSR)とフィネスを導出していきます。 まずFSRについてです。これは共振と共振の間の周波数差$\nu_{FSR}=\frac{c}{2\pi}$のことを言います。 次にフィネスについて説明していきます。これは共振器内の光がどれくら往復できるかを示したものになります。フィネスを求めるためにはFSRと透過強度ピークの半値全幅$\nu_{FWHM}$の比をとる必要があります。 そこで$\nu_{FWHM}$を求めます。これは透過光強度$P_i$を用いて求めることができます。 \begin{equation} \frac{1}{1+\frac{4r_F r_E}{(1-r_F r_E)^2}\sin^2\left(\frac{\pi L \nu_{FWHM}}{c}\right)}=\frac{1}{2} \end{equation} この式を$\frac{\pi L \nu_{FWHM}}{c}=\frac{\pi \nu_{FWHM}}{2\nu_{FSR}} << 1$として解くと$\sin$の展開ができるので \begin{equation} \nu_{FWHM}=\frac{c(1-r_F r_E)}{2\pi L \sqrt{r_E r_F}} \end{equation} となります。よってフィネス$\mathcal{F}=\frac{\nu_{FSR}}{\nu_{FWHM}}=\frac{\pi\sqrt{r_E r_F}}{1-r_E r_F}$と求まりました。 ここで共振器の分類について少しふれておきます。共振器に用いる鏡の反射率の大小関係によって三種類の分類がされます。